前言
为什么要写这个系列?
程序=数据结构+算法。
我对这句话的理解是构建程序等于解决问题。解决问题需要工具和方法,数据结构是工具,算法则是方法。
最近辞职了赋闲在家,觉得自己数据结构和算法的基础一直不牢固,于是买了本英文版的Data Structures and Algorithm Analysis in C 来加固下。我一直以为光看不练等于浪费时间,于是便想把学到的数据结构和算法亲身实现一遍,这样既熟悉了知识,又锻炼了编码能力。再者,如果能写成博客,一是做了笔记,二者能分享给大家。何乐而不为呢?
为什么选择JavaScript实现?
- 我对JavaScript不熟悉,正好借此机会来练手,以期能快速熟悉
- JavaScript能让很多应用直接通过浏览器展示出来,这样会比较直观些
这个系列主要内容是什么?
- 介绍常用的数据结构和算法的基础知识
- 介绍它们的应用,并比较它们的优劣
- 利用JavaScript实现其中的一个应用并开放源码
用到的工具有哪些?
- JS库:jQuery, EaselJS, Bootstrap, GSAP等
- CSS库:Bootstrap
- Sublime text 2进行数据结构的编码
- JSFiddle来进行JS应用的编写和调试
- MarkDown来写文章,Mou是主要的编辑器
关于本系列
文章列表
[php_everywhere]
开放源码
单链表
简介
链表即Single LinkedList。以下是维基百科的定义:
链表(Linked list)是一种常见的基础数据结构,是一种线性表,但是并不会按线性的顺序存储数据,而是在每一个节点里存到下一个节点的指针(Pointer)。由于不必须按顺序存储,链表在插入的时候可以达到O(1)的复杂度,比另一种线性表顺序表快得多,但是查找一个节点或者访问特定编号的节点则需要O(n)的时间,而顺序表相应的时间复杂度分别是O(logn)和O(1)。
根据以上定义,我们知道链表里面的每一个节点都是一致的结构,即:数据域和指向下一个的索引域。
我们定义ListNode为链表的节点类型,data为数据域,next为索引域:
function ListNode ( data ) {
this.data = data;
this.next = null;
};
和数组通过第一个元素为起始进行寻址类似,链表也需要有一个节点作为起始节点,我们将这个节点定为head,有了它,我们就能通过next域遍历到链表里的所有节点。
我们定义LinkedList为链表类型:
function LinkedList () {
this.head = null;
//use tail for efficiency
this.tail = null;
};
在以上定义中我们还保留了一个tail作为链表最后一个节点的索引。
假如我们经常要在链表的最后添加节点的话,每次都需要从head开始,遍历所有的节点直至最后一个节点,显然这样效率很低。而缓存尾节点可以使这一操作在O(1)内完成。
操作
查找
找到链表中的某个元素很简单,只需要从头结点开始逐个遍历即可。
LinkedList.prototype.find = function( element ) {
var p = this.head;
while( p != null && p.data != element ) {
p = p.next;
}
return p;
};
很显然最坏情况为查找最后一个节点和要找的元素不在链表中。平均时间复杂度为O(n)。
插入
节点后插入
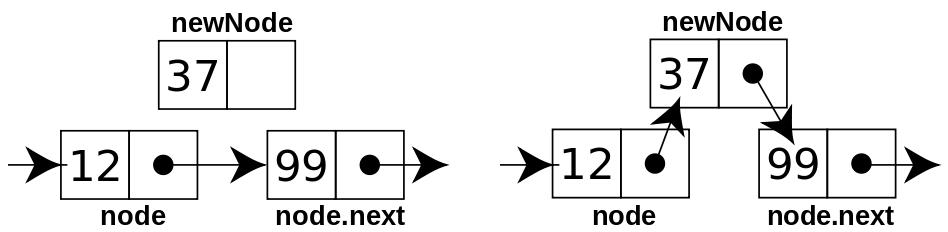
在某个节点p后插入,只需要把待插入的节点x的next指向p的next节点,然后再把p节点的next指向x即可。
LinkedList.prototype.insertAfterNode = function( element, node ) {
if( node == null ) return;
var n = new ListNode( element );
n.next = node.next;
node.next = n;
if( node == this.tail ) {
this.tail = n;
}
};
LinkedList.prototype.insertAfter = function( element, data ) {
this.insertAfterNode( element, this.find(data) );
};
节点前插入
节点前插入稍微复杂一些,这需要知道该节点之前的节点是什么。
我们需要先查找该节点之前的节点p,然后对p执行节点后插入。此中有一个特殊情况,就是节点p是头节点。
我们从头节点开始,分别用prev表示前节点,而cur表示现节点,每次遍历时都使prev等于上一次的cur,这样prev.next永远指向cur。当cur节点为需要插入的节点时,prev节点就是它前面的节点了。
LinkedList.prototype.findPrevious = function( element ) {
var prev = null;
var cur = this.head;
while( cur != null && cur.data != element ) {
prev = cur;
cur = cur.next;
}
return [prev, cur];
};
我们把头节点的特殊情况抽象出来。
LinkedList.prototype.addFirst = function( element ) {
var h = new ListNode( element );
h.next = this.head
if( this.head == null ) {
this.tail = h;
}
this.head = h;
};
最后是节点前插入:
LinkedList.prototype.insertBefore = function( element, data ) {
if( this.head == null ) return;
if( this.head.data === data ) {
this.addFirst( element );
return;
}
var p = this.findPrevious( data );
var prev = p[0];
var cur = p[1];
if( cur != null ) {
var n = new ListNode( element );
prev.next = n;
n.next = cur;
}
};
插入的最坏情况为待插入的节点为倒数第二个节点,时间复杂度为O(n)。若已知待插入节点,时间复杂度则为O(1)。
删除
删除操作跟节点后插入的操作正好相反。我们只需要找到待删除节点p的前一个节点prev,然后将prev的next指向p的next节点即可。特殊情况仍是待删除的节点为头节点,我们只需要将head指向原head的next即可。
LinkedList.prototype.delete = function( element ) {
if( this.head.data == element ) {
this.head = this.head.next;
return;
}
var p = this.findPrevious( element );
var prev = p[0];
var cur = p[1];
if( prev != null && cur != null ) {
prev.next = cur.next;
}
};
删除和插入的时间复杂度一致,若已知要删除的节点的前节点,则删除本身的操作时间复杂度为O(1)。
倒置
倒置操作是稍微需要点技巧的操作。如果你看到了这里,希望你先思考一下如何(在线性时间内)实现这个操作。
有一种直观的思路是:遍历整个链表,将每个节点的下一个节点的next域指向自己。
具体的操作为:设当前节点为p,p的next节点为q,每一次我们需要将q.next缓存到temp里,然后再将q.next指向p;然后将p移至q的位置,q移植tmp的位置,直至q为null。
最后我们需要单独对头节点进行处理,由于倒置,之前的头结点变成了现在尾节点,需要将其next指向null,然后再将头节点指向之前的尾节点,即p。
LinkedList.prototype.reverse = function() {
var p = this.head;
if( p == null ) return null;
this.tail = p;
var tmp, q = p.next;
while( q != null ) {
tmp = q.next;
q.next = p;
p = q;
q = tmp;
}
this.head.next = null;
this.head = p;
return this;
};
倒置操作需要遍历整个链表,很显然时间复杂度为O(n)。
对比和应用
通过以上操作,我们知道链表有以下特点:
- 不能执行随机索引查找,只能顺序查找
- 查找一个元素的时间复杂度为线性级O(n)
- 在已知待操作的节点时,插入和删除操作的时间复杂度为常数级O(1)
- 由于每个节点都需要储存下一个节点的索引,所以更加耗费空间
而数组的特点大多和链表相反:
- 能够执行随机查找,查找耗费时间复杂度为O(1)
- 插入和删除操作的时间复杂度为线性级O(n)
- 需要开辟一整块连续的内存空间
综上:链表不能进行随机索引查找,查找速度慢,而插入和删除的速度很快。所以适于那些不需要进行随机查找,但是频繁插入和删除的数据集。另外,由于链表的每个节点需要耗费额外空间,当数据集很大时,空间问题将会是一个可能的隐患。
链表的应用:多项式
由于链表的可以不使用连续地址的特性,使得其特别适合表达多项式,因为多项式的每项的系数不一定是连续。 而使用数组保存则可能会导致大量的空间被浪费。
每个多项式的节点都需要知道两个参数,一个是乘数,一个是多项式系数。
于是我们可以定义多项式的节点如下:
function PolyData ( cof, exp ) {
this.cof = cof;
this.exp = exp;
};
整个多项式就是一个由多项式节点组成的链表,我们可以继承自LinkedList:
function Poly( cofs, exps ) {
this.head = null;
this.tail = null;
var node;
for (var i = 0; i < cofs.length; ++i) {
node = new PolyData( cofs[i], exps[i] );
this.append( node );
};
};
Poly.prototype = new LinkedList();
Poly.prototype.constructor = Poly;
多项式之间通常有加和乘的操作,在这里就不细说了,详见Poly.js。
以下是执行两个多项式间加和乘的简易应用:


看了下教程很棒wwwwww
用JS来讲数据结构好棒,那么这样子Python也可以啦
虽然看起来比较占内存的样子~
出新系列求remind~
新文章:Stack 递归 汉诺塔 https://wuzhiwei.net/ds_app_stack/
本站RSS Feed: https://wuzhiwei.net/feed/
已订阅:P
保存为手机浏览器书签了。,-)
我打算用Java 或者Python实现基本的数据结构与算法。
你好~~~想请教一下这里代码高亮怎么弄的呢?觉得你的做得很好看~~~
WordPress插件:Crayon Syntax Highlighter
在插件的设置里面,设置主题为Monokai,这是sublime的默认主题,当然我做了一点微调,使得它看起来更像sublime些。