摘要
在这篇文章里,我将介绍二叉查找树的基本操作和应用。
我们将看到二叉查找树操作的JavaScript的递归实现。由于递归受堆栈深度的限制,我们还将考虑非递归的实现。
最后我们将其与线性表结构进行对比,总结二叉查找树的优劣和应用场景。
关于本系列
文章列表
[php_everywhere]
开放源码
二叉查找树
二叉查找树又称二叉搜索树,其维基百科的定义为:
二叉查找树(Binary Search Tree),也称有序二叉树(ordered binary tree),排序二叉树(sorted binary tree),是指一棵空树或者具有下列性质的二叉树:
- 若任意节点的左子树不空,则左子树上所有结点的值均小于它的根结点的值;
- 若任意节点的右子树不空,则右子树上所有结点的值均大于它的根结点的值;
- 任意节点的左、右子树也分别为二叉查找树;
- 没有键值相等的节点。
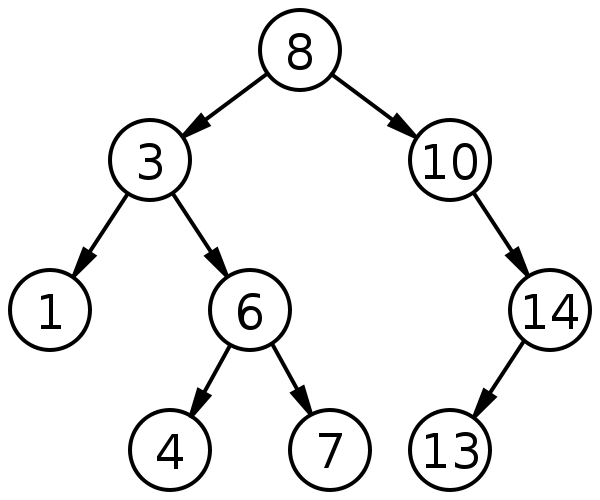
根据定义,我们知道二叉查找树中的节点最多只有两个分支,即左子树和右子树。节点需要一个键key来标明其唯一性。
我们可以定义二叉查找树的节点如下:
function BstNode(key, value, parent) {
//键
this.key = key;
//值域
this.valueList = [value];
//父节点
this.parent = parent || null;
//左节点
this.left = null;
//右节点
this.right = null;
}
以上定义还包含了parent域,用于保存节点的父节点。valueList域为值域,为一个数组,用于保存相同键下的不同值。
在一颗二叉查找树里,我们只要获取了根节点,便可遍历所有节点,故我们定义二叉查找树如下:
function BinarySearchTree() {
//根
this.root = null;
}
操作
二叉查找树的操作有很多,其基本操作为查找,插入,删除,遍历等。
由于二叉查找树的左右子树均为二叉查找树,这是一种递归的定义,所以我们可以很容易用递归的思路来操作它。
但是由于递归需要调用堆栈,一旦递归层数超过系统上限,则会堆栈溢出。所以我们也有必要了解其非递归的解法。
查找
顾名思义,二叉查找树的首要目标是查找。
递归解法
- 递归的终止条件为:当前处理的节点为空或查找成功
- 递归的缩小问题为:若当前节点比查找值小,则转至当前节点的右子树进行查找;否则转至当前节点的左子树进行查找
BinarySearchTree.prototype._find = function(node, key) {
if(node == null || node.key == key) {
return node;
}
if(node.key > key) {
return this._find(node.left, key);
}
return this._find(node.right, key);
};
非递归解法
我们可以看到递归形式的查找其实是一种尾递归,尾递归其实就是一种循环展开,所以我们不需要借助栈即可实现非递归版本的查找。
BinarySearchTree.prototype.findNR = function(key) {
var node = this.root;
while(node) {
if(node.key == key) {
return node;
}
if(node.key > key) {
node = node.left;
}
else {
node = node.right;
}
}
return node;
};
查找最小和最大节点
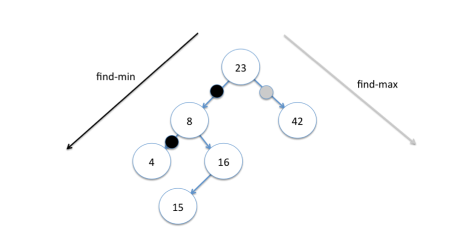
由于左子树永远小于根,右子树永远大于根,故而找到最小和最大的节点非常直观。
即,最左的节点为最小节点,最右的节点为最大节点。
由于代码相似,以下只列出找到最小节点的代码:
BinarySearchTree.prototype._findMin = function(root) {
while(root && root.left) {
root = root.left;
}
return root;
};
时间复杂度
设树的高度为h,由于查找每次都会向下下降一层,所以其时间复杂度为O(h)。
最坏的情况就是,所有左子树为空或所有右子树为空。这样,二叉查找树与单链表是一样的,树的高度跟链表长度一样为n,时间复杂度为O(n)。
如果是一颗完全二叉树,则树的高度为log(n),时间复杂度为O(log(n))。
可以证明,如果是随机构建的二叉查找树,树的高度的期望为log(n)。
插入
递归解法
插入跟查找十分类似,因为插入需要寻找到合适的节点后,然后再进行插入,所以其本身就是一种查找插入点的过程。
BinarySearchTree.prototype._add = function(node, key, value) {
//根节点特殊处理
if(this.root == null) {
this.root = new BstNode(key, value);
return ;
}
if(key < node.key) {
node.left == null ?
node.left = new BstNode(key, value, node) :
this._add(node.left, key, value);
}
else if(key > node.key) {
node.right == null ?
node.right = new BstNode(key, value, node) :
this._add(node.right, key, value);
}
else {
node.valueList.push(value);
}
};
当树中已经存在相同key的节点时,我们把值放入该节点的valueList域,以兼容同key不同值。
由于插入与查找类似,所以不列出非递归解法的代码。
时间复杂度
时间复杂度和查找相同,为O(h),h为树的高度。
最坏情况为O(n),最好情况为O(log(n)),随机插入的平均情况为O(log(n))。
删除
删除是一个比较复杂的操作,因为它有三种不同的情况:
- 待删除的节点是叶子节点(无左右子树)
- 待删除的节点只有左子树或只有右子树
- 待删除的节点既有左子树又有右子树
以下是对应的解决方法:
第一种情况最好解决,因为可以直接将其删除,而不影响树的其他部分。
第二种情况也比较好解决,因为它只有一边的子树,删除了它,我们只需要让它的那一边子树代替它原来的位置就行了。
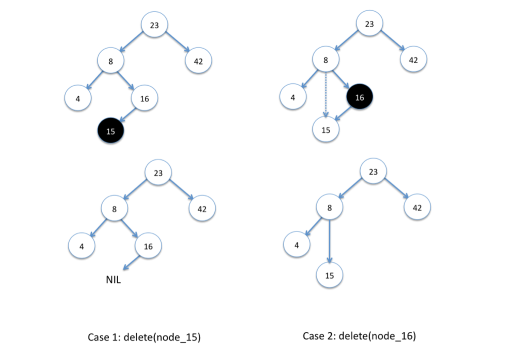
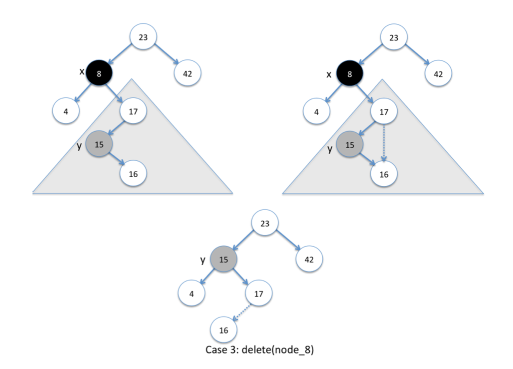
第三种情况是最复杂的,但是解决的方法却很好理解。 解决的方法是:
- 选择右子树中key最小的节点,或左子树中key最大的节点,设该节点为P
- 可以知道节点P是最接近待删节点的节点,我们将待删节点置换成节点P
- 再递归删除节点P
递归解法
BinarySearchTree.prototype._remove = function(key, value, root) {
if(!root) return null;
if(key < root.key) {
//递归一
this._remove(key, value, root.left);
}
else if(key > root.key) {
//递归二
this._remove(key, value, root.right);
}
else if(value && root.valueList.length > 1) {
root.valueList.splice(root.valueList.indexOf(value), 1);
}
//第三种情况
else if(root.left && root.right) {
var rightMin = this._findMin(root.right);
root.key = rightMin.key;
root.valueList = rightMin.valueList;
//递归三
this._remove(root.key, null, root.right);
}
//第一种和第二种情况合并处理
else {
var next = root.left ? root.left : root.right
if(root == this.root) {
this.root = next;
this.root.parent = null;
return;
}
if(root.key >= root.parent.key) {
root.parent.right = next;
}
else if(root.key < root.parent.key) {
root.parent.left = next;
}
if(next) {
next.parent = root.parent;
}
}
return root;
};
非递归解法
在递归解法中,我们看到有三处递归。
其中前两次递归都是在查找待删除的节点,这与查找的非递归是一样的;而最后一次的递归则出现在第三种情况里,其实我们只需要深入分析一下第三种情况,即可避免递归。
以选取右子树的最小节点为P举例,我们可以肯定P没有左子树,这就退化到了第二种情况。这时候删除P,只需要将P的右子树连接到P的父节点即可。
由于代码大部分类似,以下将不给出非递归代码。
时间复杂度
删除操作分为两部分:
- 查找待删除的节点,其时间复杂度就是查找的时间复杂度,为O(h),h为树高度;
- 执行删除操作,我们可以通过非递归解法看到三种情况的删除,都只需要常数级别的操作即可完成,故其时间复杂度为O(1)。
所以删除操作的时间复杂度为O(h),h为树的高度,与查找,插入相同。
中序遍历
中序遍历的意思是指按照左子树->根->右子树的顺序对树进行遍历。
由于二叉查找树的特殊结构,对其进行中序遍历,可以获得一个升序的序列。
递归解法
按照中序遍历的描述可以很自然的想到递归解法。
- 递归的终止条件为:当前节点为空节点
- 递归的缩小方法为:分别对当前节点的左子树和右子树进行递归
BinarySearchTree.prototype._inOrderTravel = function(root, func) {
if(root) {
this._inOrderTravel(root.left, func);
func(root);
this._inOrderTravel(root.right, func);
}
};
非递归解法
也许非递归解法才是一个真正的挑战,在阅读下文之前,建议读者拿出纸笔,设想如何用非递归解法来对二叉查找树进行中序遍历。
在前文中,我们知道递归其实就是一种函数调用,该调用需要用到栈来保存递归进入时当前的变量,称之为调用栈。
其实递归转换为非递归的解法关键就在于:我们自建一个调用栈,来保存进入递归时的当前变量。
仔细观察递归的代码。
- 若当前节点有左子树,则需要对左子树进行递归。此时,调用栈需要把当前节点入栈以备返回时使用;
- 若当前节点没有左子树,则可以直接遍历当前节点。需要判断当前节点是否有右子树:
- 若有右子树,则将当前节点设为右节点,继续遍历;
- 若没有右子树,说明对当前节点的处理工作结束,需要进行递归返回。此时,若调用栈不为空,我们将调用栈出栈,遍历出栈节点,直至其有右子树。
BinarySearchTree.prototype.inOrderTravelNR = function(func) {
var node = this.root;
var stack = [];
while(node) {
if(node.left) {
stack.push(node);
node = node.left;
}
else {
func(node);
while(! node.right) {
node = stack.pop();
if(! node) {
return ;
}
func(node);
}
node = node.right;
}
}
};
时间复杂度
我们设具有n个节点的二叉查找树的中序遍历时间复杂度为T(n),设左边有k个节点,则右边有n-k-1个节点。
故而:
可以得出:
所以中序遍历的时间复杂度为O(n)。
应用
二叉查找树的应用十分广泛。
C++里的map和set就是基于二叉查找树的原理实现的。
由于二叉查找树的特殊结构,导致其十分适合于动态查询的数据系统。
因为所有的数据在插入之后便成为有序序列,而且二叉查找树的插入,查找,删除的平均时间复杂度为O(log(n)),这是非常高效的。
设想一个系统,需要频繁插入、删除数据,获取分段有序序列,获取排名等等。如果用数组等实现的话,每一次插入删除后都需要重新排序,才能获取有序序列。而二叉查找树则可以在插入删除时,动态的调整树,使其输出仍为一个有序序列。
然而二叉查找树的最坏情况,将其退化为单链表,从而导致其效率急剧下降。故而二叉查找树需要进行一定的修正才能运用于实际场合。
对比
| 查找 | 随机访问 | 插入 | 删除 | 有序访问 | 需要排序 | |
|---|---|---|---|---|---|---|
| 二叉查找树 | O(log(n)) | 不支持 | O(log(n)) | O(log(n)) | 支持 | 不需要 |
| 数组 | O(n) | 支持 | O(n) | O(n) | 支持 | 需要 |
| 单链表 | O(n) | 不支持 | O(1) | O(1) | 支持 | 需要 |
| 字典 | O(1) | 支持 | O(1) | O(1) | 不支持 | 需要 |
总结
二叉查找树由于其构造的特性,使得其特别适合于需要动态查询的数据结构。
由于二叉查找树中序遍历即为有序序列,也使得其适合需要经常排序的数据结构。
但是二叉查找树存在最坏情况,即左右子树为空和输入为有序序列,这时,二叉查找树退化为单链表,丧失其所有优势。
我们需要对二叉查找树进行平衡化处理,使得其形态与平衡二叉树靠近,从而达到避免最坏情况的出现。
