在RTS游戏中,寻路是相对容易的,A*算法可以较高的效率寻到最优解,改变一下估值函数,也可以用更快的速度寻找到次优解,所以寻路在大多数时候并不是问题所在。
假设一个集群,需要从位置A移动到位置B,中间充满了各种障碍,如何移动才显得比较自然?这是一个比较困难的问题。
有一种方案是给每个集群中的单位都做一次寻路,但是寻路算法开销较大,如果集群中的单位较多则会面临性能问题。另一种方案是进行一次寻路,从A到B,然后考虑一种方式使得集群沿着该路径进行移动。
初步的想法很简单,所有单位全部沿路径移动即可。但是由于单位众多,而路径只有一条线,这样所有单位变会在这条线上互相挤压,导致观感很不自然且效率很低。
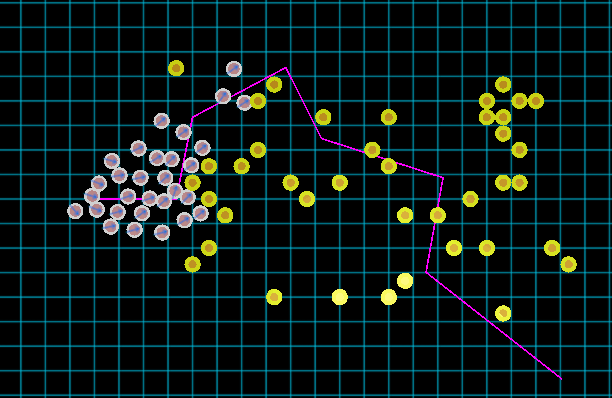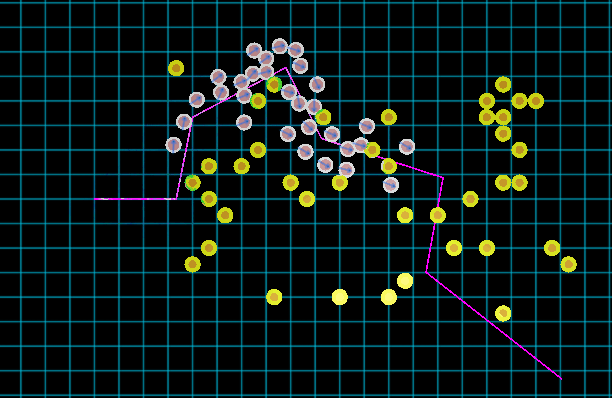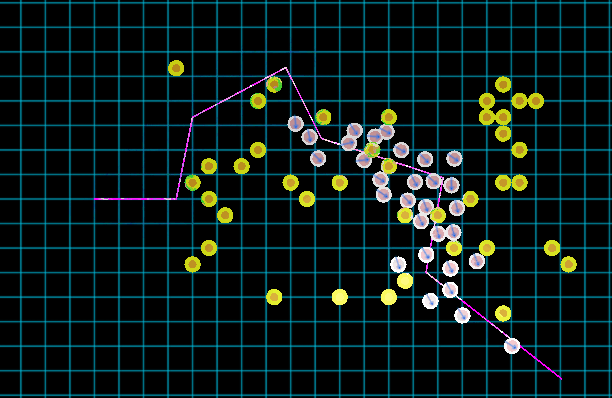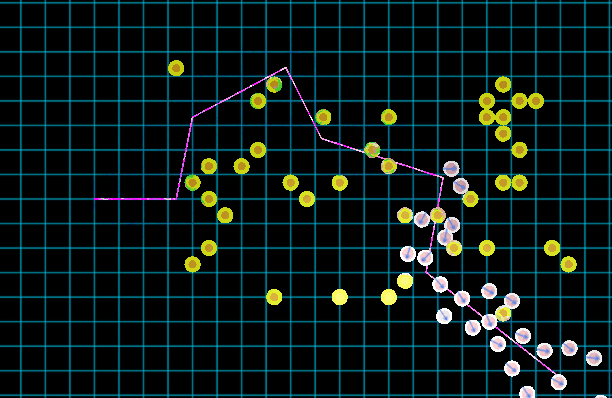
上图便是一个相对较为自然的集群沿路径移动的效果图,而本文将阐述其背后的方法。
在上世纪80年代,Craig W. Reynolds便提出了一系列集群移动的分解方法,其将看似很复杂无规律的集群移动分解为多个不相干的小型移动算法。这些算法都被称为Steer算法,在其发表的文章Steering Behaviors For Autonomous Characters中有详细的介绍。
为了简化运算,我们假定所有的单位和障碍都为圆,圆心为其质点。
通道跟随
对我们最有启发的便是Path Following Steer,与跟随一条线状路径不同,其定义了一个有宽度的通道,集群将沿着这条通道移动。
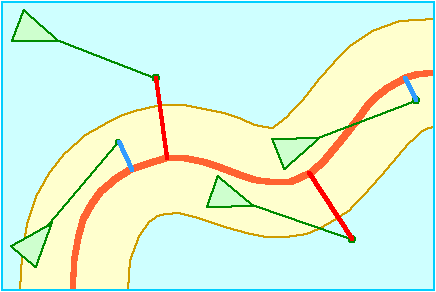
与线不同,通道具有宽度,就跟马路一样,这样所有单位不会拥挤在一条线上,从而使得竞争更少,移动也更加自然一些。
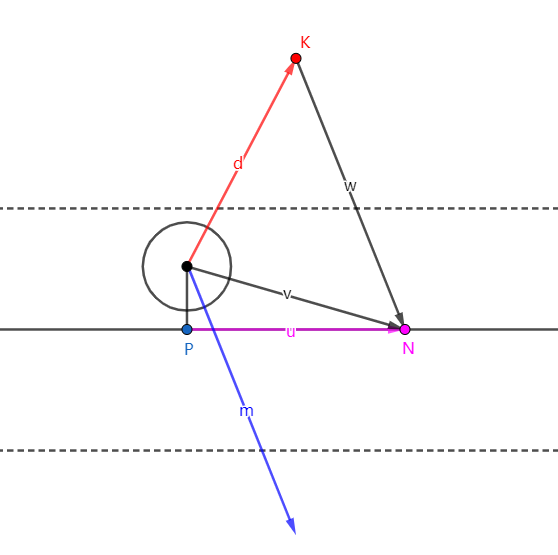
如上图所示,中间一条实线为路径线,上下两条虚线为通道的边界,圆为一个正在移动的集群单位。红色向量$\vec d$为这个单位此刻的方向向量,K为下一帧的预期位置,P为其在路径上的投影点,N为从P点沿着路径向前移动$|\vec d|$所得的点,向量$\vec v$为单位质点指向N点的向量。
计算K到路径的投影距离便可知其大于路径宽度,所以K点在通道范围之外。如果按照预期方向,单位将会跑出通道,所以此时我们需要向单位施加一个通道跟随向量。这个向量即为$ \vec v – \vec d = \vec m$,我们把蓝色的修正向量$\vec m$与当前方向向量$\vec d$相加便可得到经过通道跟随修正的方向向量。
如果K点在通道内,则说明下一帧单位不会移出通道,这时候我们不需要对单位的方向向量做通道跟随的修正,即$\vec m = 0$。
避障
躲避静态障碍
对于静态障碍,行军单位需要躲避,以免发生碰撞。
首先,我们需要确定是否会发生碰撞,与哪个障碍发生碰撞。这个比较简单,只需要拿下一帧的预期位置与各个障碍物的质点算距离。如果距离小于单位和障碍的半径和,我们便可知单位与该障碍即将发生碰撞。这一步的距离计算可以求平方以避免距离的开方的开销。
如果预期发生碰撞,那我们便需要对行进方向再次做出修正,这个Steer叫做Obstacle Avoid Steer。
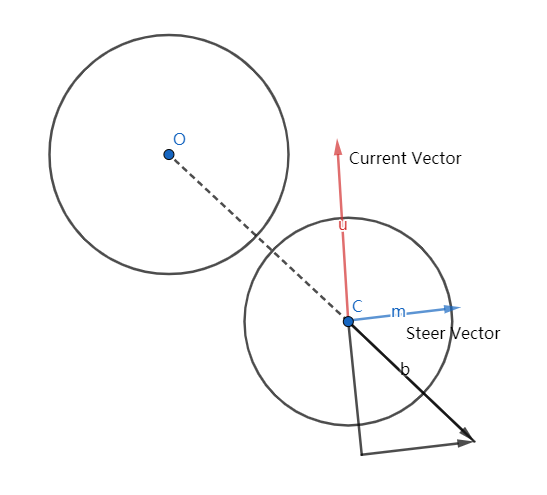
如上图所示,当前方向向量为$\vec u$,我们取单位质心C与障碍质心O的反向连线向量为$\vec b$,则避障的修正向量$\vec m = \vec b – \vec u$。
与同伴保持距离
在行进过程中,行军单位还需要与同伴保持一定距离,以免互相发生碰撞。
这个Steer叫做Separation,其与Alignment和Cohesion组合可以模拟令人信服的鸟群或者其他集群的运动效果,这些算法的集合叫做Flocking。
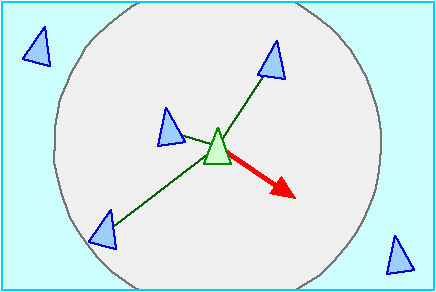
Separation的原理是搜集自身一定范围内的同伴,然后将其搜索到的同伴与自身连线的反方向的方向向量做加权相加,这个权重一般取为1/r,r为与同伴的距离。可以用以下公式表示: $$ \vec S = \vec V_1 / r_1 + \vec V_2 / r_2 + … + \vec V_n / r_n $$
Unity Demo
本文只粗略了阐述了思想,并没有附上具体代码。为此我上传了一个Unity的Demo到Github,文章开头的效果图便是出自该Demo。
Demo地址:https://github.com/iWoz/path_follow_steer。

大佬你好,请问这个文章用到的算法,是参考了哪篇论文吗?想要拜读一下
不好意思,我刚看到这个参考文献了,谢谢大佬