前言
在阅读本文之前,请先看一道题:求解x,使得 $e^{-x}-x = 0$
如果你能用纸笔解出这道题的话,请务必留言告知我方法,谢谢。
如果你不能用纸笔解出这道题的话,那么我们可以完全借助代码来对其进行求解。
以下就是我写的求解器,它几乎能够对所有的一元函数进行自动求解。
你可以在输入框内尝试任意一元函数,按Enter键或点击求解按钮进行求解。如有bug请留言,谢谢。
它的原理有一点复杂,下面将会一一讲到。
牛顿法
牛顿法是求解的核心方法,它的维基百科的定义为:
牛顿法是一种在实数域和复数域上近似求解方程的方法。方法使用函数f(x)的泰勒级数的前面几项来寻找方程f(x)=0的根。
简言之,牛顿法就是对x进行迭代,直至x收敛于某个很小的范围。
其迭代的公式为:$$x_{n+1} = x_n – \frac{f(x_n)}{f'(x_n)}$$ 其中${f'(x_n)}$为${f(x_n)}$的导函数。
要理解牛顿法,你就要了解泰勒展开。牛顿法其实是利用了一阶的泰勒展开:$$f(x) = f(x_0)+(x -x_0)\cdot f'(x_0)$$ 对上述方程 $f(x) = 0$ 进行求解,得到: $$x = x_0 – \frac {f(x_0)}{f'(x_0)}$$ 这就是牛顿迭代公式的逼近原理。
你可以通过这幅图直观的看到x逼近的过程:
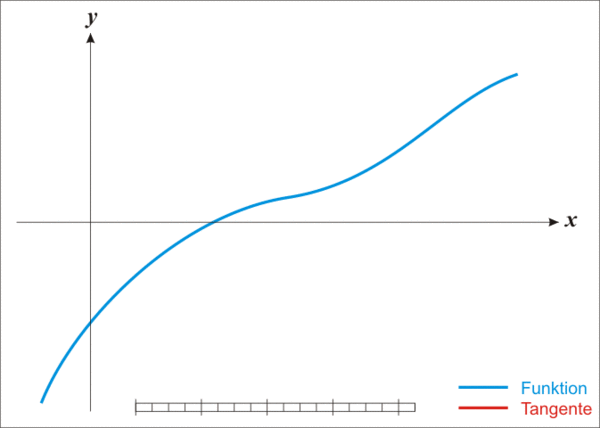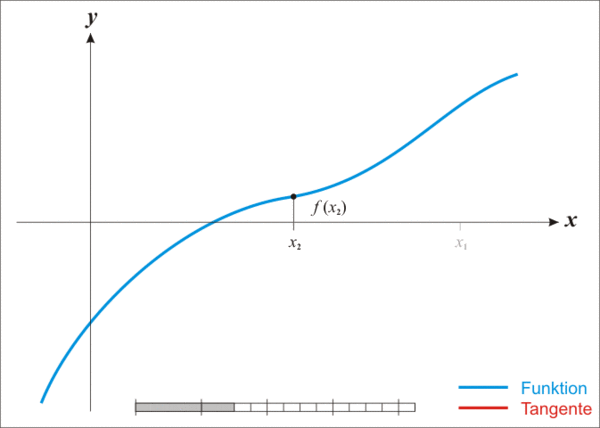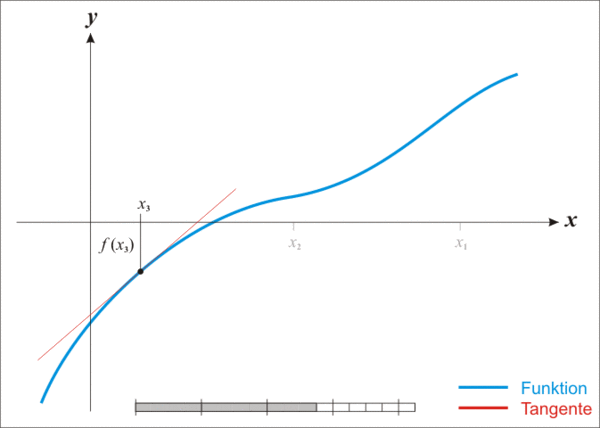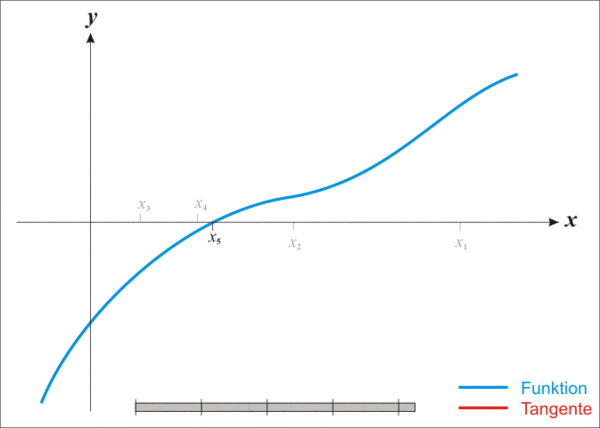
所以,对于任意的一元函数,我们都可以尝试用牛顿法来求得其近似解,一个简单伪代码如下:
声明 x0, x1, i
//当误差小于10^-9时,或者迭代步数超过10^5时,迭代结束
while (Math.abs(x0 - x1) > 10E-9) {
//进行迭代
x0 = x1
x1 = x0 - (f(x0) / f'(x0))
//记步
++ i
//若步数过长,终止迭代
if( i < 10E5) {
break
}
}
以下,我们将根据牛顿法,来构建自动求解器。
构建求解器
在构建求解器时,有几个关键问题需要解决:解析输入的表达式,表达函数,求导函数方程,对函数进行代入求值。
其中,最优先的一个问题是:我们怎么储存(表达)函数?
《SICP》的第一章提到了一种表示法:二分表达树。
以下是表达式((5 + z) / -8) * (4 ^ 2)的二分表达树的图例:
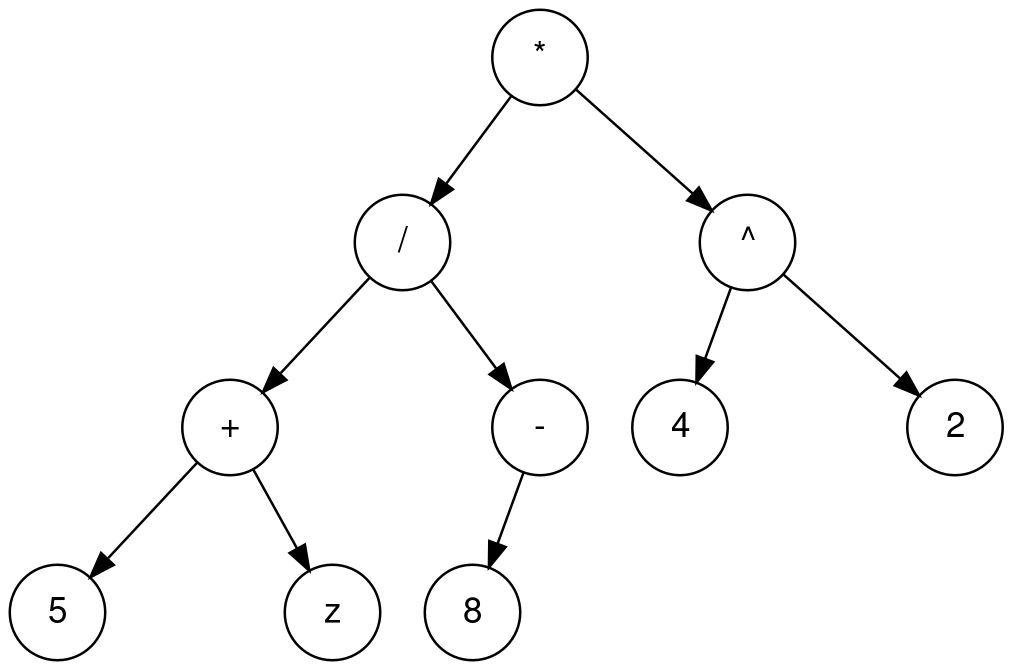
为什么选择这种表达方式呢?
主要是因为它是树形结构,方便递归处理节点,而我们之后求导函数其实就是用的递归思路,包括代入求值也是递归的思路。
预处理表达式
首先,我们需要预处理输入的表达式字符串。因为在数学中有一些简略或者多余的写法需要在此规范化。
例如:
5x表示5*x,通常都省略了乘号.5+x表示0.5+x,省略了小数点前的0-x中的-其意思是取负操作,是一个单目运算符。为了不与减法冲突,我们也需要将其预处理为(0-x)+5-x的加号完全没有意义,我们需要将其省去
比如,输入串 .5e^-x-2x,经过预处理后将变成 0.5e^(0-x)-2x。
自然的输入串经过预处理后,就应该是一个中缀的表达式字符串,这是人类能够自然理解的表达式形式。
但是为了将表达式储存成二叉表达树,我们还需要将中缀表达式转换成后缀表达式。
由迪杰斯特拉提出的调度场算法可以解决这个问题。
调度场算法
调度场算法基本和我们在栈 递归 汉诺塔文中提到的利用栈来计算表达式的方法类似。
它用队列表达输出的后缀表达式,利用了栈来储存操作符和函数。
其详细算法过程为(摘录自维基百科):
- 当还有记号可以读取时:
- 读取一个记号。
- 如果这个记号表示一个数字,那么将其添加到输出队列中。
- 如果这个记号表示一个函数,那么将其压入栈当中。
- 如果这个记号表示一个函数参数的分隔符(例如,一个半角逗号 , ):
- 从栈当中不断地弹出操作符并且放入输出队列中去,直到栈顶部的元素为一个左括号为止。如果一直没有遇到左括号,那么要么是分隔符放错了位置,要么是括号不匹配。
- 如果这个记号表示一个操作符,记做o1,那么:
- 只要存在另一个记为o2的操作符位于栈的顶端,并且
- 如果o1是左结合性的并且它的运算符优先级要小于或者等于o2的优先级,或者
- 如果o1是右结合性的并且它的运算符优先级比o2的要低,那么
- 将o2从栈的顶端弹出并且放入输出队列中(循环直至以上条件不满足为止);
- 然后,将o1压入栈的顶端。
- 只要存在另一个记为o2的操作符位于栈的顶端,并且
- 如果这个记号是一个左括号,那么就将其压入栈当中。
- 如果这个记号是一个右括号,那么:
- 从栈当中不断地弹出操作符并且放入输出队列中,直到栈顶部的元素为左括号为止。
- 将左括号从栈的顶端弹出,但并不放入输出队列中去。
- 如果此时位于栈顶端的记号表示一个函数,那么将其弹出并放入输出队列中去。
- 如果在找到一个左括号之前栈就已经弹出了所有元素,那么就表示在表达式中存在不匹配的括号。
- 当再没有记号可以读取时:
- 如果此时在栈当中还有操作符:
- 如果此时位于栈顶端的操作符是一个括号,那么就表示在表达式中存在不匹配的括号。 将操作符逐个弹出并放入输出队列中。
- 退出算法。
其分支逻辑比较繁琐,需要细细阅读和小心实践。
构建二叉表达式树
假设输入表达式为:(a+b) * (c * (d+e)),经过调度场算法,我们得到a b + c d e + * *的后缀表达式。
此时我们便可以利用后缀表达式的特点,快速的构建出一颗二叉表达树来。
构建的算法很简单:
- 新建一个栈
- 从头到尾遍历后缀表达式,
- 当发现操作数时,我们将其存为操作数节点,入栈;
- 当发现操作符时,我们将其存为操作符节点,
- 若是二元操作符,我们将栈顶的两个节点弹出,作为该操作符的节点左右节点,然后将该节点入栈
- 若是一元操作符,我们将栈顶节点弹出,作为该操作符的右节点,然后将该节点入栈
整个过程如果用图来说明,会十分容易理解。
- 首先我们遍历到
a,它是操作数,入栈,b也是操作数,也入栈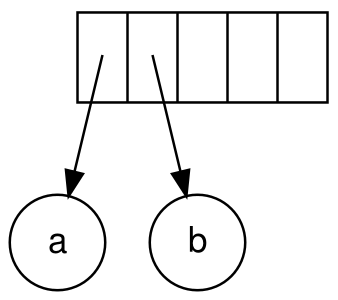
- 遍历到
+,它是二元操作符,弹出两个节点,然后添加至左右节点,入栈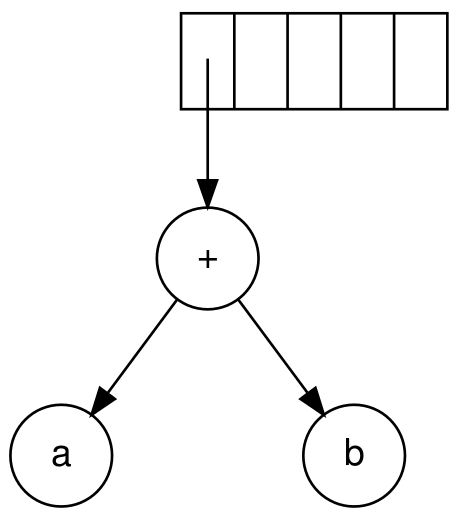
- 接下来三个都是操作数,将它们都入栈
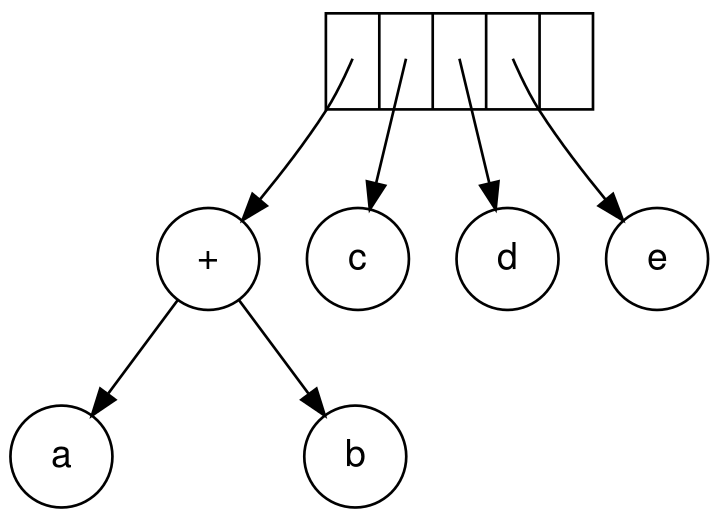
- 然后遍历到
+,同2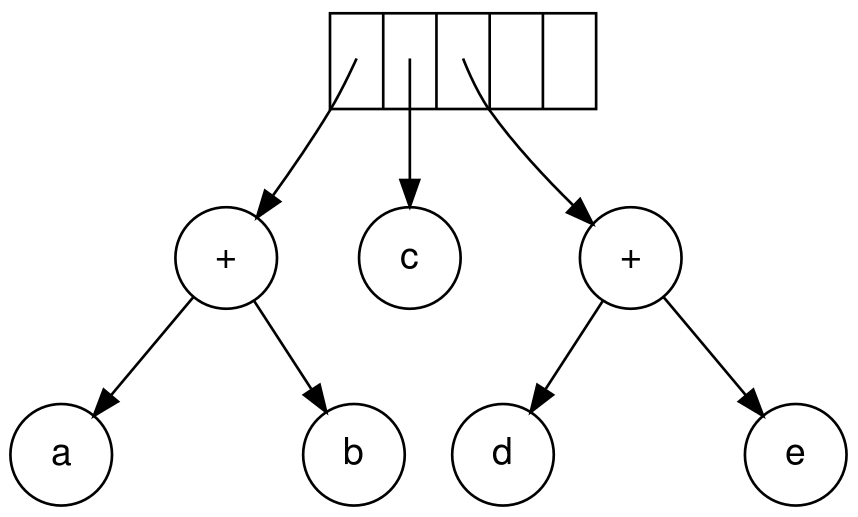
- 接下来是
*,同2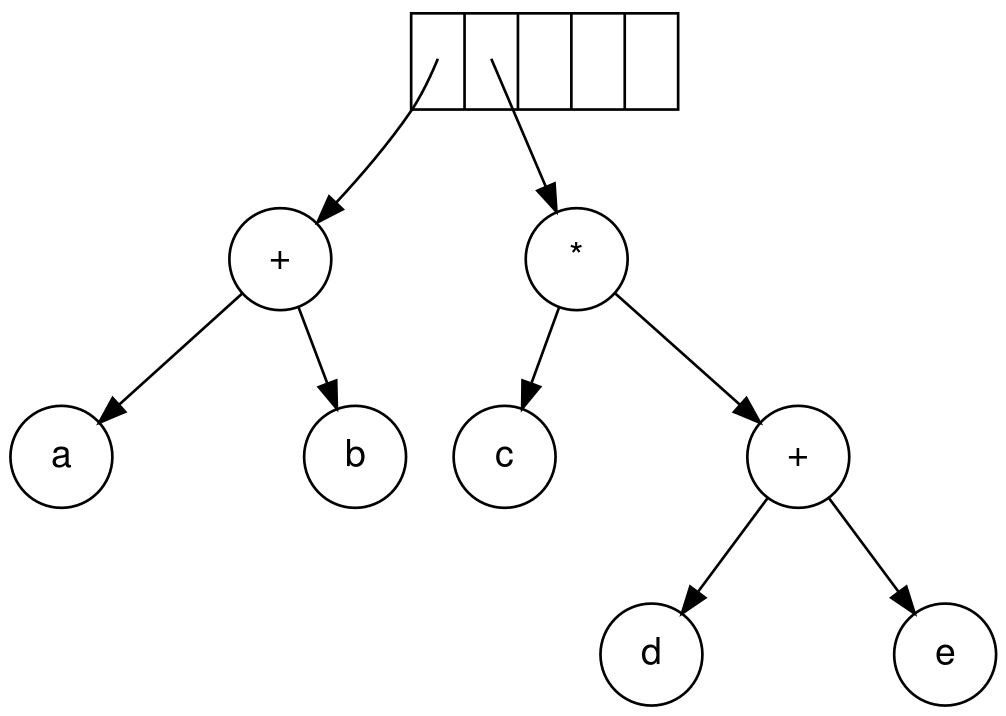
- 仍然是
*,同2;遍历完毕,我们得到如下的二叉表达树: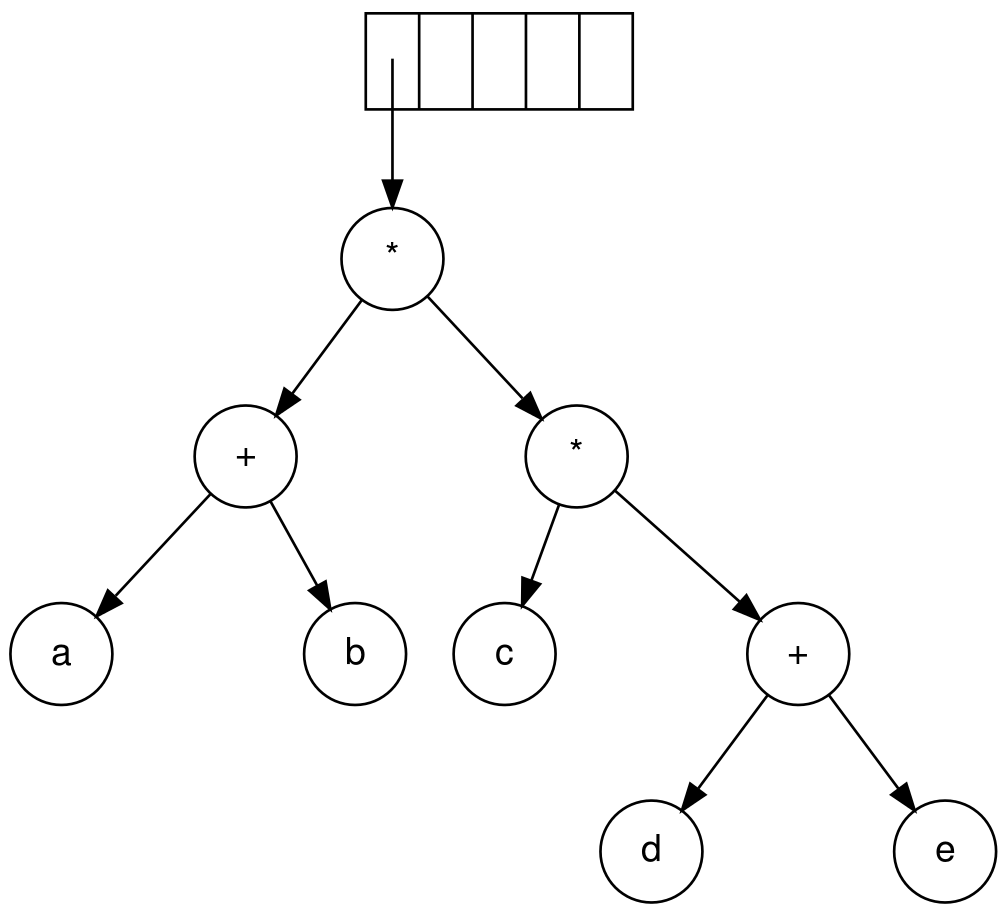
我们定义二叉表达树为如下:
/**二叉表达树*/
function ExpTree(key) {
//根节点
this.root = null;
//未知量的表达形式,默认为x
this.key = key || 'x';
//中序遍历的字符串
this.infix = '';
//后续遍历的字符串
this.postfix = '';
}
定义树的节点如下:
/**二叉表达树节点*/
function ExpTreeNode(key, left, right) {
//节点值
this.key = key;
//左子树,默认为空
this.left = left || null;
//右子树,默认为空
this.right = right || null;
}
求值
对二叉表达树进行代入求值的算法应该很容易就能想到。
利用二叉树的递归特性,根为操作符或函数,左子树右子树是递归定义。我们只需要将左右子树的值递归求出,然后在进行操作符运算即可。
代码如下:
/**递归计算表达式的值*/
ExpTree.prototype.cal = function(node, x) {
if(!node) {
return;
}
//有子树,进行递归运算
if(node.left || node.right) {
//进行操作符运算
return this.op( node.key, this.cal(node.left, x), this.cal(node.right, x) );
}
//否则,直接返回节点值
switch(node.key) {
case 'x':
return x;
case 'e':
return Math.E;
case 'pi':
return Math.PI;
default:
return node.key;
}
};
/**执行原子计算*/
ExpTree.prototype.op = function(opr, left, right) {
switch(opr) {
case '+':
return left + right;
case '-':
return left - right;
case '*':
if(left == 0 || right == 0) {
return 0;
}
return left * right;
case '/':
return left / right;
case '^':
return Math.pow(left, right);
case 'sin':
return Math.sin(right);
case 'cos':
return Math.cos(right);
case 'tan':
return Math.tan(right);
case 'cot':
return 1 / Math.tan(right);
case 'arcsin':
return Math.asin(right);
case 'arccos':
return Math.acos(right);
case 'arctan':
return Math.atan(right);
case 'ln':
return Math.log(right);
case 'log':
return Math.log(right) / Math.log(left);
default:
//error!
console.log(opr, 'error!');
return 0;
}
};
构建导函数树
至此,我们只剩下了求解导函数的步骤。这一步也是比较复杂的操作,因为导函数的规则实在是很多。
请参见导函数的维基百科的定义。
但是重点是,我们用什么方法来求解导函数,又该如何表达导函数呢?
首先,表达导函数应该用二叉表达树来进行表示,因为可以直接对其进行代入求值,而且二叉表达树具有递归的特性;
其次,由于二叉表达树的根节点总是操作符或函数的特性,左右子树也是表达式,我们可以用递归的思路来求解导函数。
主要思路为: 对于一个二叉表达树,根节点为操作符或函数,左右子树则为操作符或函数的运算的参数。
比如根节点为+操作,左右子树为a,b:

具体的表达式则为 $a + b$,我们对加法求导法则是$(a+b)’ = a’ + b’$。我们可以发现求导也可以递归表达。即上面那颗二叉树的导函数为根为+,左子树为a的导函数的树,右子树为b的导函数的树。
所以我们可以用递归来表示求导的过程,下面是完全规则的求导代码:
ExpTree.prototype.dao = function(node) {
if(!node) {
return;
}
var t;
switch(node.key) {
case '+':
case '-':
//(l+r)' = l' + r'
//(l-r)' = l' - r'
t = new ExpTreeNode(node.key, this.dao(node.left), this.dao(node.right));
break;
case '*':
//(l*r)' = l'*r + l*r'
t = new ExpTreeNode('+');
t.left = new ExpTreeNode('*', this.dao(node.left), node.right);
t.right = new ExpTreeNode('*', node.left, this.dao(node.right));
break;
case '/':
//(l/r)' = (l'*r - l*r') / (r*r)
t = new ExpTreeNode('/');
t.left = new ExpTreeNode('-');
t.left.left = new ExpTreeNode('*', this.dao(node.left), node.right);
t.left.right = new ExpTreeNode('*', node.left, this.dao(node.right));
t.right = new ExpTreeNode('*', node.right, node.right);
break;
case '^':
t = new ExpTreeNode('*');
if(node.right._containParam(node.right)) {
//(l^r)' = (l^r) * (ln(l)*r)'
t.left = node;
t.right = this.dao(new ExpTreeNode('*', new ExpTreeNode('ln', null, node.left), node.right));
}
else {
//(l^c)' = (l'*c) * l^(c-1)
t.left = new ExpTreeNode('*', this.dao(node.left), node.right);
t.right = new ExpTreeNode('^', node.left, new ExpTreeNode('-', node.right, new ExpTreeNode(1)));
}
break;
case 'sin':
//sin(r)' = cos(r)*r'
t = new ExpTreeNode('*');
t.left = new ExpTreeNode('cos', null, node.right);
t.right = this.dao(node.right);
break;
case 'cos':
//cos(r)' = 0-sin(r)*r'
t = new ExpTreeNode('-', new ExpTreeNode(0));
t.right = new ExpTreeNode('*', new ExpTreeNode('sin', null, node.right), this.dao(node.right));
break;
case 'tan':
//tan(r)' = r' / (cos(r) * cos(r))
t = new ExpTreeNode('/', this.dao(node.right));
t.right = new ExpTreeNode('*', new ExpTreeNode('cos', null, node.right), new ExpTreeNode('cos', null, node.right));
break;
case 'cot':
//cot(r)' = 0-r'/(sin(r)*sin(r))
t = new ExpTreeNode('-', new ExpTreeNode(0));
t.right = new ExpTreeNode('/', this.dao(node.right));
t.right.right = new ExpTreeNode('*', new ExpTreeNode('sin', null, node.right), new ExpTreeNode('sin', null, node.right));
break;
case 'arcsin':
//arcsin(r)' = r' / (1-r*r)^0.5
t = new ExpTreeNode('/', this.dao(node.right))
t.right = new ExpTreeNode('^', null, new ExpTreeNode(0.5));
t.right.left = new ExpTreeNode('-', new ExpTreeNode(1), new ExpTreeNode('*', node.right, node.right));
break;
case 'arccos':
t = new ExpTreeNode('/', this.dao(node.right))
t.right = new ExpTreeNode('^', null, new ExpTreeNode(0.5));
t.right.left = new ExpTreeNode('-', new ExpTreeNode(1), new ExpTreeNode('*', node.right, node.right));
t = new ExpTreeNode('-', new ExpTreeNode(0), t);
//arccos(r)' = 0 - (r' / (1-r*r)^0.5)
break;
case 'arctan':
t = new ExpTreeNode('/', this.dao(node.right))
t.right = new ExpTreeNode('+', new ExpTreeNode(1), new ExpTreeNode('*', node.right, node.right));
//arcsin(r)' = r' / (1+r*r)
break;
case 'ln':
//ln(r)' = r'/r
t = new ExpTreeNode('/', this.dao(node.right), node.right);
break;
case 'log':
//log(l,r) = r'/(r*ln(l))
t = new ExpTreeNode('/', this.dao(node.right));
t.right = new ExpTreeNode('*', node.right, new ExpTreeNode('ln', null, node.left));
break;
case 'x':
//x' = 1
t = new ExpTreeNode(1);
break;
default:
//常量的导数为0
t = new ExpTreeNode(0);
break;
}
return t;
};
最终计算
我们把导函数表达成了二叉表达树的形式,至此,我们已经把所有问题全部解决。
求解表达式解的过程将十分清晰:
- 将输入的表达式构建成表达式树
t,同时构建其导函数的表达式树dt - 利用牛顿法,进行迭代求解
开放源码
源码地址为:https://github.com/iWoz/DSinJS/blob/master/ExpressionTree/ExpTree.js。
源码集成在JavaScript的算法与数据结构系列中,托管于GitHub:
Demo托管于JsFiddle。
欢迎讨论!

有点意思,如果有求解析解的就霸气了。
求微分的英文单词是derivation
开个玩笑,如果我能求解析解,我将会获得图灵奖或菲尔兹奖。
举个栗子,一元高阶方程至今没有解析解的解法。
你看文章很仔细,估计你也有强迫症。。但是我人比较懒,所以就写成了
daoBTW,微分的英文是Differential,导数的英文是derivative。这两者是不同的概念。
坚持更新博客就像坚持写日记一样,不仅是习惯,也是耐力,表示支持
猩猩,赞一个!怎么开始研究数值计算了- –
没有专门研究,瞎折腾而已~
很赞,我收录到工具里面来了。
最后附有贵博客地址:http://www.atool.org/function_solver.php
你好,2个bug
1. x=0
说是格式不对
2. x^(x+1)=0
这个解不了
最好增加一个功能:求解范围的指定,例如仅求解(a,b)开区间内的解。
当然不指定求解区间的功能还是保留下来。