日常生活中，你能看到各种各样的球类。

当球与平面发生碰撞时，球会改变其行进的轨迹，由于摩擦，也会改变行进的速度。

在2D游戏中，我们通常把球抽象为一个圆，把平面抽象为一条线。生活中的球和平面的碰撞，就简化成了圆和线的碰撞。

在本文，我们将看到怎么利用向量运算来解决一般的圆线碰撞问题，最后将会有一个DEMO来检验我们的成果。

不要害怕，一切东西都将很简单基础。你只需要保持好舒服的姿势，最好面前有一张纸和一根笔，然后端上一杯水（少喝点碳酸饮料），让我们开始吧~

向量及其运算

定义

向量是一个同时具有大小和方向的几何对象。

字面上的定义总是那么的不容易理解，结合下图，一个以A为起点，B为终点的有向线段。它描述的就是向量$\vec{AB}$。

然而向量和有向线段是有区别的，因为有向线段还需要一个起点，而向量不需要，它只需要终点和起点的相对位移，即可以定义它的大小和方向。

我们可以定义向量$\vec{AB}$为:

vab = { vx:B.x - A.x, vy:B.y - A.y };

有向线段实际是起点+向量，我们将有向线段的起点定义为p0，终点定义为p1。

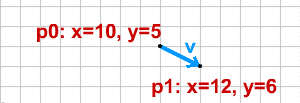
我们可以将以上的有向线段定义为：

ab = {
p0:{x:10, y:5},
p1:{x:12, y:6},
vx:p1.x - p0.x,
vy:p1.y - p1.y
};

生活中墙可以简化为一条有向线段，球的移动轨迹也可以简化为一条有向线段。

即p0为球当前所在的位置，p1为下一时刻球应该在的位置，所以{vx, vy}就是球的速度向量。

向量运算

向量之间可以像数字一样进行很多运算，运算规则比较简单，然而却能带来很大的便利性。下文将讲述向量的几个基本运算以及它们的意义和应用。

单位向量

单位向量就是其长度为1的向量。

向量的长度其实就是两点距离的问题。

v.len = math.sqrt(v.vx*v.vx + v.vy*v.vy);

而由单位向量的定义，易知v的单位向量为：

v.dx = v.vx / v.len;
v.dy = v.vy / v.len;

单位向量就是是一个纯指向性质的向量，其便利在于不需要去额外计算它的长度，它的长度永远为1。

加法

如果学过初中物理，你们应该对向量的加法不陌生。没错，向量加法就是用来求合力时的运算。 如图：

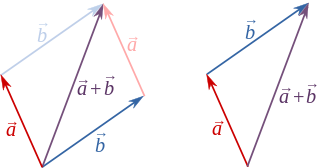
$\vec{c} = \vec{a} + \vec{b}$在程序中$\vec{c}$可以用如下方式表达：

c = {vx:a.vx+b.vx, vy:a.vy+b.vy};

向量加法的意义在于：有多个向量作用于同一点时，可以通过其来计算出所有向量作用下合成的一个向量，将多个向量简化为一个向量。

点积

点积是向量间的乘积，其结果是一个标量（纯数字，不带方向信息）。其定义为：

$\vec{A} \cdot \vec{B} = |\vec{A}|\ |\vec{B}|\ cos\theta，其中\theta为 \vec{A}和\vec{B}的夹角$。

求解点积的代码为：dp = A.vx*B.vx + A.vy*B.vy

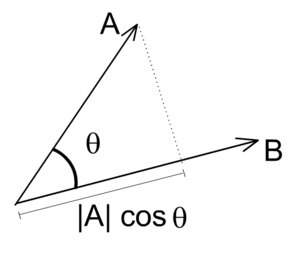
由cos函数的性质，可以知道如果夹角为90度，则点积为0；夹角超过90度，则点积小于0；夹角小于90度，则点积大于0。

其意义为可以快速的判断两向量指向的方向是不是相近。若点积大于0，则相近，小于0，则相反。

投影

向量$\vec{A}$在$\vec{B}$上的投影向量就是：

一个向量长度为$\vec{A}$在$\vec{B}$方向上投影长度，向量方向为$\vec{B}$方向的向量。

其实，你只需要参照点积的图，看到$|\vec{A}|\ cos\theta$，就是$\vec{A}$在$\vec{B}$上的投影长度。

投影长度乘$\vec{B}$的单位向量，则为向量$\vec{A}$在$\vec{B}$上的投影向量。

所以$\vec{A}$在$\vec{B}$上投影向量为$(|\vec{A}|\cos\theta)\ \vec{DB}$，其中$\vec{DB}$为$\vec{B}$的单位向量。

我们可以利用点积来简化运算，$\vec{A} \cdot \vec{DB} = |\vec{A}|\ |\vec{DB}|\ cos\theta$，由于$\vec{DB}$为单位向量，所以$(|\vec{A}|\cos\theta)\ \vec{DB} = (\vec{A} \cdot \vec{DB}) *\vec{DB}$ 代码如下：

function getProjectVector(u, dx, dy) {
var dp = u.vx*dx + u.vy*dy
return {vx: dp*dx, vy: dp*dy}
}

叉乘

叉乘也是向量间的乘积，但是其结果仍然是一个向量。

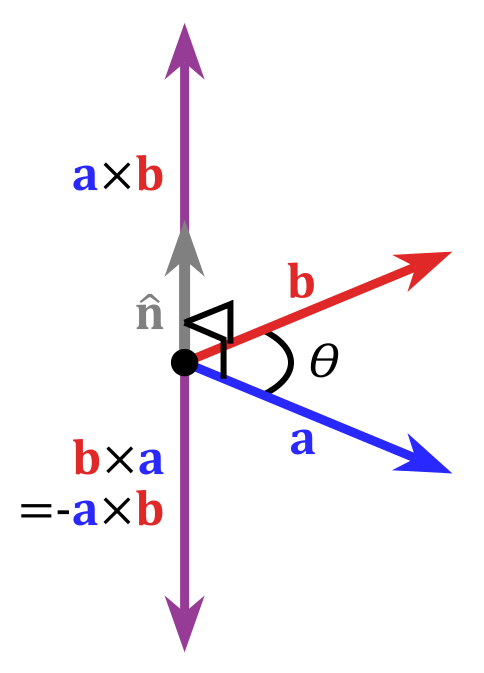
叉乘的一个重要便利在于：它能用来判断点在向量的哪边。若点在向量的左边，则夹角小于180度；若点在向量的右边，则夹角大于180度。

以下是利用叉乘（矩阵运算），来获知点c是否在有向线段ab的左侧。

//判断点c是否在线段ab的左侧
function isLeft(a, b, c) {
return (b.x - a.x) * (c.y - a.y) - (b.y - a.y) * (c.x - a.x) < 0;
}

注意：在以上代码中判断的是$<0$，是因为本文中DEMO使用的坐标系的Y轴朝向是朝下递增，如果是正常的坐标系朝向，即Y轴朝上递增，应该判断的是$>0$。

法向量

法向量是与向量方向垂直的向量。对于每条向量它都有左右两条法向量。想象你的眼睛和屏幕构成了一个向量，如果你坐姿正确的话，张开你的双手，你左手就是左法向量，右手就是右法向量。

因为法向量与原向量垂直，所以其点积为0，fx*vx + fy*vy = 0，最简单的解为{fx:-vy, fy:vx}和{fx:vy, fy:-vx}。

若点在向量左边，则叉乘小于0，则$vx * fy – vy * fx < 0$。

由上易知左法向量为：{fx:vy, fy:-vx}，右法向量为：{fx:-vy, fy:vx}。

一般来说，我们更希望用单位向量来表示法向量。

所以我们可以将v的右法向量表示为：

v.rx = -v.dy
v.ry = v.dx

同理，左法向量表示为：

v.lx = v.dy
v.ly = -v.dx

坐标更新

在游戏引擎中都有一个每帧循环，循环在每一帧调用一次来更新游戏逻辑。

对于圆的行进更新，很自然会想到每帧将圆的位置从p0更新到p1。

但是这么做是不准确的，因为程序的帧率不会恒定，也就意味着每帧的间隔时间是不一样的。

举个栗子：假设你的引擎设定的FPS是50，即每秒有50帧，每帧你想移动的距离是1px，这样球每秒将会移动50px。但是由于还有其他的运算和渲染，引擎的FPS只能达到40，这样球每秒只能移动40px，跟你的预期完全不一样。

如果球在规定时间内的位置和你的预期不符，那样会导致很多的问题。

解决办法是利用每帧的间隔时间乘与移动速率来得到下一帧的位置。

碰撞

当圆在行进过程中，我们必须判断圆是否与线段发生碰撞。而确定碰撞的方式也很直观，就是确定圆心与线段的距离是否小于圆的半径。

而且发生碰撞之后，我们需要将圆的位置回移到其恰好与线相交的那点。

任意移动线段的两点，若圆线相交，则圆变为半透明，绿色的线段为圆需要回移的有向线段。

注意，当圆碰撞到线段的两端时，其回弹向量的大小为圆与线段端点的距离；否则为圆与线段的距离。

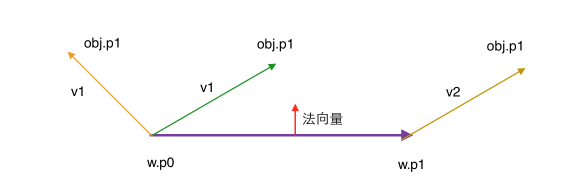
第一步，我们设圆的位置为obj.p1，墙为有向线段w。

我们将墙的起点w.p0和obj.p1的向量称为v1向量，将墙的终点w.p1和obj.p1的向量称为v2向量。

第二步，若v1与w的点积小于0（夹角大于90度，最左侧情况），或v2与w的点积大于0（夹角小于90度，最右侧情况），则可知圆碰撞到了线段的两端。返回的碰撞向量为v1或v2。

若前两种情况都不符合，则圆碰撞到了线段内。这时，我们只需要返回v1在w的法向量上的投影向量即可。

第三步，若返回的向量的长度小于圆的半径，则说明发生了碰撞。

代码如下：

//获取圆与线段的碰撞修正向量
function getIntersectVector(obj, w) {
var v1 = {vx:obj.p1.x-w.p0.x, vy:obj.p1.y-w.p0.y};
if(v1.vx*w.vx + v1.vy*w.vy < 0) {
return v1;
}
var v2 = {vx:obj.p1.x-w.p1.x, vy:obj.p1.y-w.p1.y};
if(v2.vx*w.vx + v2.vy*w.vy > 0) {
return v2;
}
if(isLeft(w.p0, w.p1, obj.p0)){
return getProjectVector(v1, w.lx, w.ly);
}
return getProjectVector(v1, w.rx, w.ry);
}

反弹

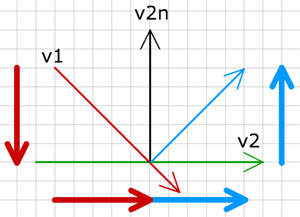
由上图可以清晰的知道，回弹向量沿墙壁(v2)的投影向量与v1沿墙壁(v2)的投影向量一致，而回弹向量沿墙壁法向量(v2n)的投影向量与v1的刚好相反。

所以，我们只需要求出v1的以上两个投影向量，即可得到反弹的向量。

代码如下：

//获取回弹向量
function getBounceVector(obj, w) {
var projw = getProjectVector(obj, w.dx, w.dy);
var projn;
var left = isLeft(w.p0, w.p1, obj.p0);
if(left) {
projn = getProjectVector(obj, w.rx, w.ry);
}else {
projn = getProjectVector(obj, w.lx, w.ly);
}
projn.vx *= -1;
projn.vy *= -1;
return {
vx: w.wf*projw.vx + w.bf*projn.vx,
vy: w.wf*projw.vy + w.bf*projn.vy,
};
}

DEMO

拖拽红色圆球，然后释放给与其方向，即可测试。

有关代码托管于Github:

问题

以上方法的问题在于：若圆球的速度过快，则会下一帧判断的时候，直接穿越了墙壁，而没有检测到碰撞。

这个问题有两种解决方案：一种是预测圆线的碰撞，并进行相应的处理；还有一种是对每帧的时间进行切片，如果时间切片足够小的话，则在一个时间切片内圆的移动不会超过其直径，则避免了穿越墙壁的情况。

下面是时间切片方案的伪代码：

// 每帧更新，delta为每帧时间
function update(delta) {
// pre code...
// 球碰撞更新
// 做切片
var minTimeGap = VECTOR_MIN_TIME_GAP; // 时间切片的单元
var maxTimeCutGap = VECTOR_MAX_CUT_TIME_GAP; // 一帧内最后切剩下的时间如果超过此值也做一次碰撞
var totalDelta = 0;
var segment = Math.floor(delta / minTimeGap)
if (segment < 1){
segment = 1;
}
for (var i = 1; i <= segment; i++) {
totalDelta = totalDelta + minTimeGap;
checkCollison(minTimeGap); // 做一次碰撞检测
}
if (delta - totalDelta >= maxTimeCutGap) {
checkCollison(delta - totalDelta); // 剩余时间再做一次碰撞检测
}
// post code...
}

P.S. 推荐一个可以直观理解线性代数的视频集合，非常nice：http://space.bilibili.com/88461692/#!/channel/detail?cid=9450。